PID制御(Xcos)：積分(I)動作

積分動作の詳細を見ます。

特徴

積分動作は、次式で表されます。

入力に単位ステップを与えた場合下図のように時間に比例して出力は大きくなります。

積分動作

比例(P)動作における出力と、積分(I)動作の出力が等しくなる時間を積分時間(T_I)と言います。
図からも分かるように積分時間が長くなれば傾きが小さくなります。
つまり、出力変化が小さくなります。
逆に積分時間が短くなれば、出力変化は大きくなります。

PI(比例＋積分)動作

PI 調整器の操作量は、

で表されます。

この式をラプラス変換すると次式になります。

これをブロック線図にすると下図になります。

参考

とした場合

積分動作を含んだ場合のオフセット値を見ます。
PV(s) の式は、

で求まります。

十分長い時間経過後の式を最終定理を用いて導きだします。

＜最終値の定理＞
t→∞ における値は、s を掛けてからs→0としたものと等しい

したがって、オフセットは 0 となります。

このことから、オフセットを無くすには積分(I)動作を加えれば良いことが分かる。

PI制御の例

下図のようなPI制御されている系に単位ステップを入力します。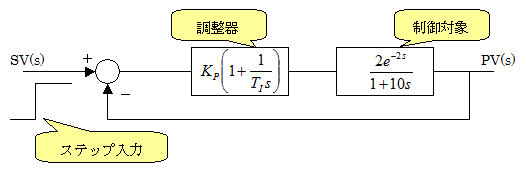

積分時間T_I = 10Sec で K_P＝1、K_P＝2 とした場合の出力をシミュレーションで見ます。

比例動作の時と同じようにムダ時間をパデ近似で求めます
＜パデ近似の設定＞

コンソール画面

-->s=%s;                  //←多項式の変数 s を定義
-->exec('pade_s.sci');    //←pade_s関数の使用を宣言(関数が記述されているファイル名を指定)
-->[num,den]=pade_s(2,4)  //パデ近似の分子・分母を s の多項式で取得
 den  =
                    2    3   4  
    105 + 105s + 45s +10s + s   
 num  =
                    2     3   4  
    105 - 105s + 45s - 10s + s

＜ブロック線図＞

比例要素との違いは、積分要素（青色の破線円）を追加したことです。

＜実行結果＞

時間→∞でオフセットが無くなることが分ります。