伝達関数：poly,syslin,csim

前ページでは、伝達関数*入力をラプラス逆変換し、求めた式を用いてグラフ表示させました。
ここでは、面倒な作業は、Scilab　に任せ、伝達関数のみを使用してグラフ表示させます。

伝達関数から直接グラフ表示

コンソール画面

-->t=linspace(0,8,100);    //←時間変数　ｔ　へ　0～8秒　を100分割した値の配列を設定
-->s=poly(0,'s');          //←多項式の変数　s　を定義
-->G=1/(s^2+3*s+2);        //←伝達関数　G　を定義
-->sys=syslin('c',G);      //←連続時間線形システムへ伝達関数 G を登録
-->y=csim('step',t,sys);   //←伝達関数　G　へステップ入力を与えた場合の出力変化を　y　に得る
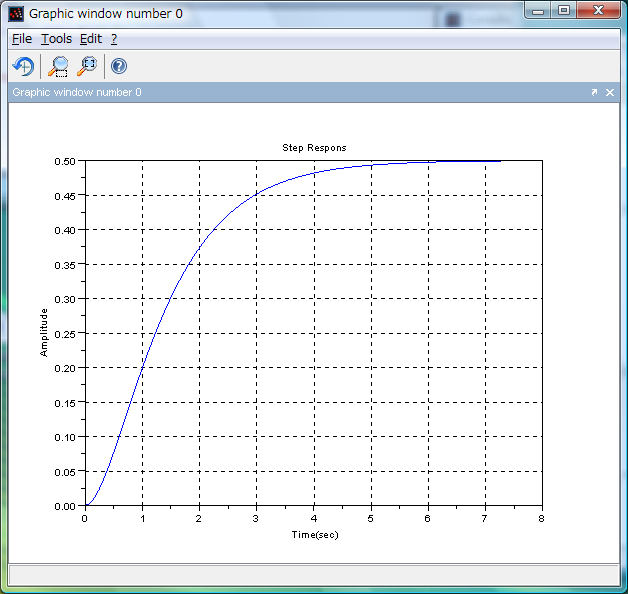
-->plot(t,y)               //←グラフ表示
-->xgrid()                 //←グリッドの表示
-->xtitle('Step Respons','Time(sec)','Amplitude')  //←タイトル関連の表示

前ページと全く同じグラフが得られました。

poly()

poly　は、多項式を定義するときに使います。

poly(0,'s')	s と言う文字をシンボリックに使うことを宣言
poly([-1 2],'x')	配列は、多項式の根 x の多項式で、 -1 と 2 の根を持つ式を取得この場合　-2-x+x²　が得られる
poly([1 2 3],'t','coeff)	配列は多項式の係数この場合　1+2t²+3t³ が得られる

＜実行例＞

コンソール画面

-->G=1/(s^2+3*s+2)
       !--error 4     //←多項式の定義を試みたが　s　を定義していない為エラー発生
Undefined variable: s

-->s=poly(0,'s')     //←多項式の変数　s　を定義
 s  =
    s   
 
-->G=1/(s^2+3*s+2)   //←今度は、多項式の定義に成功
 G  =
        1        
    ---------    
              2  
    2 + 3s + s

コンソール画面

-->f1=poly([-1 2],'x')            //←根が -1 と 2 の多項式を求める
 f1  =
             2  
  - 2 - x + x                     //← -2-x+x^2 が得られた・・・(x-2)(x+1) 

-->f2=poly([1 2 3],'x','coeff')   //←係数が 1、2、3 の多項式を求める
 f2  =
               2  
    1 + 2x + 3x                   //← 1+2x+3x^2 が得られた

syslin()、csim()

syslinは、伝達関数の登録コマンドです。
csimは、単位ステップ応答法の結果を出力するコマンドです。

sys=syslin('c',G)	連続時間線形システムへ、関数 G を登録その線形システム上での関数 G を sys とする＜第1パラメータ＞ 'c'=連続時間線形システム 'd'=離散時間線形システム
y=csim('step',t,sys)	線形システムへ登録された関数　sys　へステップ入力( t秒 )を与えた場合の出力変化を　y　に得る＜第1パラメータ＞ 'step'=ステップ応答法の結果を出力 'impuls'=インパルス応答法の結果を出力