伝達関数：ステップ応答法

代表的な制御要素であるステップ応答の特性を見ていきます。

比例要素

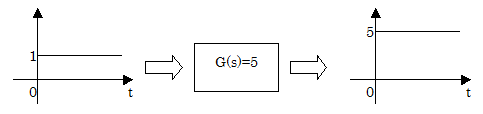
伝達関数が次式で表されるものを比例要素と言います。

G(s) = K

Kは比例定数と言います。

微分要素

伝達関数が次式で表されるものを比例要素と言います。

G(s) = Ts

しかし、この要素実現することは、事実上不可能です。
（ステップ入力の 0→1 変化が 0秒、つまり微分すると無限大になるため）

そこで、近似的に次式を利用します。

コンソール画面

-->t=linspace(0,8,100);     //←時間変数　ｔ　へ　0～8秒　を100分割した値の配列を設定
-->step=linspace(1,1,100);  //←ステップ入力値・・・tと同じ要素数分の 1 を用意
-->s=poly(0,'s');           //←多項式の変数 s を定義
-->G=s/(s+1)                //←近似微分要素の伝達関数
 G  =
      s     
    -----   
    1 + s   

-->sys=syslin('c',G)        //←連続時間線形システムへ、関数 G を登録
 sys  =
      s     
    -----   
    1 + s   

-->y=csim(step,t,sys);      //←sys へステップ入力( t秒 )を与えた場合の出力変化を　y　に得る
-->plot(t,y)
-->xgrid()
-->xtitle('Step Respons','Time(sec)','Amplitude')

＜実行結果＞

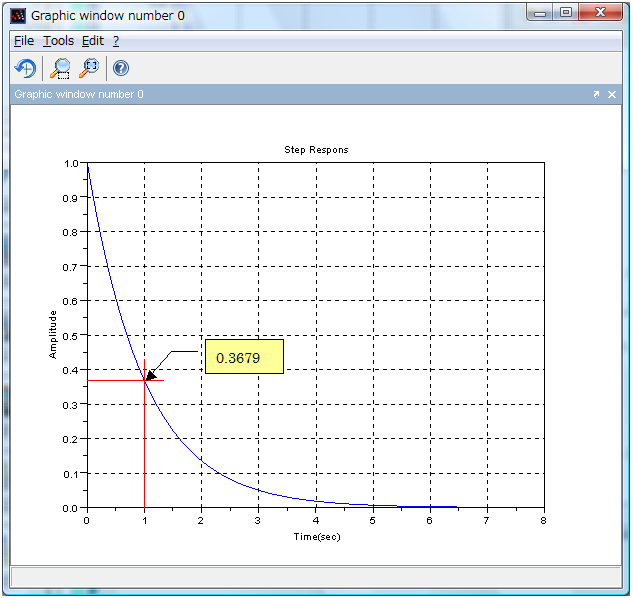
Y(s) を出力、X(s) をステップ入力とすると次の式が成り立ちます。

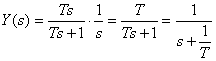
これをラプラス逆変換してy(t)を求めます。

この式からも分かるように、ｔ＝T のとき 1/e となり 0.3679 が得られます。
単位ステップ入力に対して 0.3679 の出力になる T を時定数と言います。

注　意

最初、ステップ応答を見るために csim('step',t,sys) として、第一パラメータに 'step' の文字列を与えて確認しました。
しかし、結果は　0 → -1.0 のグラフになりました。
1.0 → 0 の表示にどうしても出来なかったので、step と言う配列にx軸個の1を用意して、それをステップ入力としました。
もっとスマートな方法があると思いますが、ヨッパな私には分かりませんでした。
もし、ご存知の方が居られましたら、ご教授願いますm(_~_)m

積分要素

伝達関数が次式で表されるものを積分要素と言います。

T=1 のときのステップ応答を Scilab でシミュレーションさせます。

コンソール画面

-->t=linspace(0,8,100);     //←時間変数　ｔ　へ　0～8秒　を100分割した値の配列を設定

-->G=1/s                    //←積分要素の伝達関数
 G  =
    1   
    -   
    s   
 
-->sys=syslin('c',G)        //←連続時間線形システムへ、関数 G を登録
 sys  =
    1   
    -   
    s   
-->y=csim('step',t,sys);      //←sys へステップ入力( t秒 )を与えた場合の出力変化を　y　に得る
-->plot(t,y)
-->xgrid()
-->xtitle('Step Respons','Time(sec)','Amplitude')

＜実行結果＞

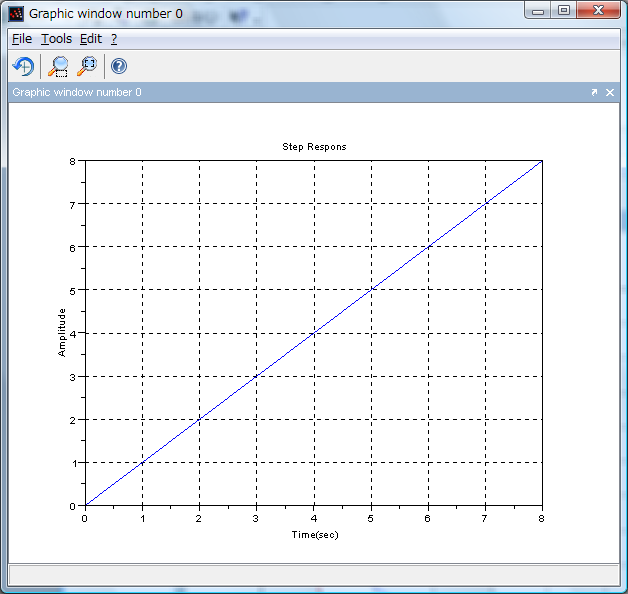
Y(s) を出力、X(s) をステップ入力とすると次の式が成り立ちます。

これをラプラス逆変換してy(t)を求めます。

ｔ＝T で出力が 1 になることが分かります。

１次遅れ要素

伝達関数が次式で表されるものを１次遅れ要素と言います。

この系では言葉通り、位相が送れて出力されます。

T=1 のときのステップ応答を Scilab でシミュレーションさせます。

コンソール画面

-->t=linspace(0,8,100);     //←時間変数　ｔ　へ　0～8秒　を100分割した値の配列を設定
-->s=poly(0,'s');           //←多項式の変数 s を定義
-->G=1/(s+1);               //←積分要素の伝達関数
-->sys=syslin('c',G)        //←連続時間線形システムへ、関数 G を登録
 sys  =
      1     
    -----   
    1 + s   

-->y=csim('step',t,sys);      //←sys へステップ入力( t秒 )を与えた場合の出力変化を　y　に得る
-->plot(t,y)
-->xgrid()
-->xtitle('Step Respons','Time(sec)','Amplitude')

Y(s) を出力、X(s) をステップ入力とすると次の式が成り立ちます。

ラプラス逆変換を行っていきます。

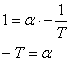
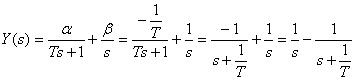
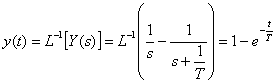
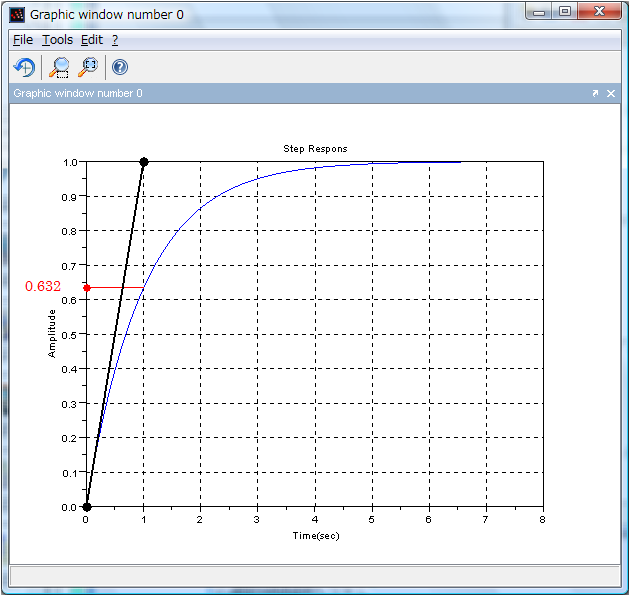
得られた式でｔ＝T のとき y(t)＝0.632 になります。
このときの T の時間を時定数と呼びます。
また、原点における接線が定常値と交わる時間でもあります。