PID制御(Xcos)：PID・ボード線図

PI 動作と PID 動作wをボード線図から見ます。

PI動作

下ブロック線図で示される、PI動作の一巡伝達関数のボード線図を見ます。

コンソール画面

-->s=%s;                     //←多項式の変数 s を定義
-->exec('pade_s.sci');       //←pade_s関数の使用宣言
-->[num,den]=pade_s(0.5,4);  //←ムダ時間0.5Secのパデ近似を取得
-->G=(1.2 * 1/(8*s) + 1.2) * 2 * 1/(1+5*s)^3 * num/den; //←ブロック線図を式に変換
-->sys=syslin('c',G)         //←連続時間線形システムへ一巡伝達関数Gを登録
-->bode(sys,1e-3,1e2,0.01)   //←ボード線図の作図
-->g_margin(sys)             //ゲイン余裕 1.7359002dB
 ans  =
    1.7359002
 
-->p_margin(sys)             //←位相余裕 7.2419195°
 ans  =
    7.2419195

＜ボード線図＞

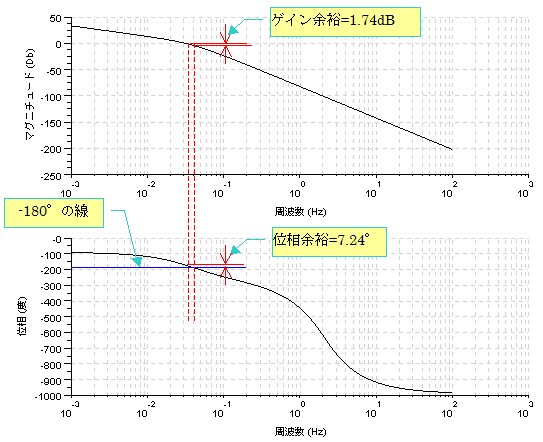
ゲイン、位相ともあまり余裕が無いことが分ります。

PID制御

次に微分動作を加えたPID制御を見ます。
微分動作の追加以外は、PI動作と同じ設定です。

コンソール画面

-->s=%s;                     //←多項式の変数 s を定義
-->exec('pade_s.sci');       //←pade_s関数の使用宣言
-->[num,den]=pade_s(0.5,4);  //←ムダ時間0.5Secのパデ近似を取得
-->G=(1.2 * 1/(8*s) + 1.2 + 1.2*(5*s)/(1+0.5*s)) * 2 * 1/(1+5*s)^3 * num/den; //←ブロック線図を式に変換
-->sys=syslin('c',G)         //←連続時間線形システムへ一巡伝達関数Gを登録
-->bode(sys,1e-3,1e2,0.01)   //←ボード線図の作図
-->g_margin(sys)             //ゲイン余裕 13.066654dB
 ans  =
    13.066654
 
-->p_margin(sys)             //←位相余裕 58.014393°
 ans  =
    58.014393

＜ボード線図＞

微分動作を追加することでゲイン、位相の余裕が大幅に改善されているのが分ります。

PI・PIDのステップ応答

下図ブロック線図を作成し、前述のPI、PID制御（フィードバック）のステップ応答を見ます。

＜実行結果＞

このステップ応答からも、微分動作の追加が有効であることが分ります。