 |
はじめに
数学の準備
高校数学
複素数
ラプラス変換
ラプラス逆変換
Scilab入門
概要
四則演算
配列
グラフ表示
プログラム1
プログラム2
伝達関数
 概要
概要poly,syslin,csim
ステップ応答法
RLC回路
周波数応答
ゲイン・位相
ボード線図
比例・微分・積分
1次遅れ,ムダ時間
パデ近似の導出
pade関数の作成
制御の安定性
ブロック線図
フィードバック
2次遅れ系
ステップ応答法
周波数応答法
ナイキスト線図
安定性の判別
判別の仕組み
安定余裕の評価
評価の例題
Xcos
入門
例・運動方程式
PID制御(Xcos)
概要
比例(P)動作
積分(I)動作
微分(D)動作
PID・ボード線図
伝達関数:概要
制御システムは、幾つかの要素から構成されています。
その動特性を表す方法として入出力間の関係を表す伝達関数 G(s) を用います。
このとき伝達関数は、ラプラス変換された s 領域における入出力信号の比になります。
初期条件は、0 とします。

運動方程式を使った例
伝達関数を例を使って求めてます。下図のような、ばねとダンパと台車がつながった系を考えます。

| m | 質量[kg] 加速度に比例し生ずる慣性力の比例乗数 |
| c | ダンパの減衰係数[kg/s] 速度に比例して効く減衰力の比例定数 |
| k | ばね定数[kg/s2] 釣り合った点からのずれに比例した復元力の比例定数 |
| f | 外力[kgm/s2] |
| x | 変位[m] |
この系の数学表現は、次式(運動方程式)となります。
| ・・・(a) |
求めたい伝達関数 G(s) は、外力 F(s) を加えたときの変位量 X(s) の関数です。
| 伝達関数 | 変位量 | |
| 外力 |
(a)式をラプラス変換します。

伝達関数では初期値を 0 とすることを約束していたので x(0) = 0 となり、次式が得られます。
これから伝達関数 G(s) が求まります。
外力のラプラス変換 F(s) に伝達関数 G(s) を乗じたものがラプラス変換された変位 X(s) になることが分かります。
つまり、外力 F(s) にどのような力を入力するかによって、出力 X(s)が決まります。
入力関数
上でモデル化したシステムをステップ応答を用いて調査します。ステップ応答とは、f(t) = h の関数で表せられる入力関数です。
グラフで書くと下図になります。

h = 1 とした場合、この式をラプラス変換すると、変換表から次式が得られます。
| L(1)= |
この式が F(s) になります。
解析

例で提示したシステムを解析するためにそれぞれの値を次のように決めます。
- m = 1 [kg]
- c = 3 [kg/s]
- k = 2 [kg/s2]
X(s)=F(x)・G(x) は前述しました。
この式をラプラス逆変換すれば変位量 x(t) を求めることが出来ます。
ラプラス逆変換を求め易いように、部分分数展開を行います。
ここで
なので
s = 0 と置くとαが求まります。

同様に s = -1 とするとβが求まります。
最後に s=-2 とするとγが求まります。

得られた α・β・γ を X(s) 式 に代入すると次のようになります。

この式をラプラス変換表を用いてラプラス逆変換を行います。
出力 y(t) の式が得られました。
グラフ表示
得られた式を視覚的に捕らえるため Scilab を使ってグラフ表示します。| コンソール画面 |
-->t=linspace(0,8,100); //←時間変数 t へ 0〜8秒 を100分割した値の配列を設定
-->y=0.5*exp(-2*t)-exp(-t)+0.5; //←y(t) の式
-->plot(t,y) //←グラフ表示
-->xgrid() //←グリッドの表示
-->xtitle('Step Respons','Time(sec)','Amplitude') //←タイトル関連の表示
|
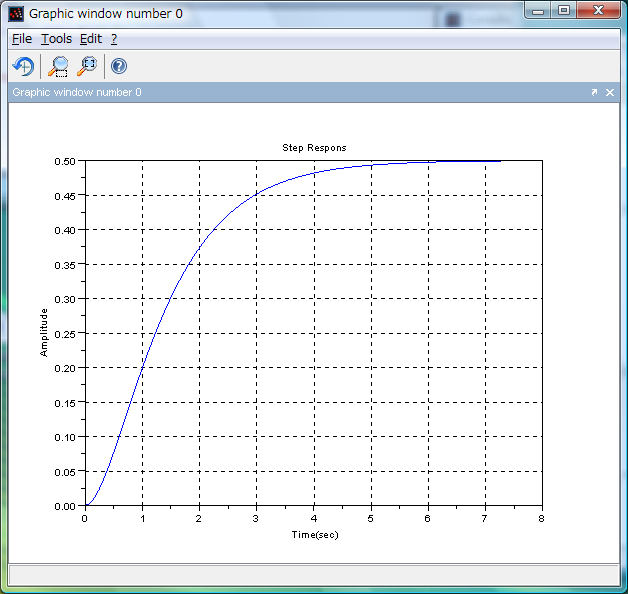
上で得た式を t→∞ で極限をとれば 0.5 になることが分かります。
グラフの結果と一致しています。